Issue 032, April 25, 2022

Megan K. Puglia, Ph.D., Senior Research Chemist

The electrical and thermal properties of a material are important design considerations for the engineering of myriad systems and applications.

In metals, both electrical and thermal conductivity are heavily influenced by the mean free path of an electron. Thermal conductivity is a material’s ability to transfer heat through itself via the movement and collisions of electrons. Discontinuities in the crystalline lattice such as particles, solute, and interfaces introduce scattering sites that shorten the mean free path, reducing thermal conductivity. Lattice vibrations also decrease thermal conductivity via the scattering of these free moving electrons. Higher temperatures increase lattice vibrations and therefore decrease conductivity. Commonly used units of thermal conductivity are W/(m∙K) or W/(m∙˚C). Electrical conductivity, the ease with which electrons travel through a material, has units of S/m or %IACS, as outlined in a previous Tech Brief.¹

German physicists Gustav Wiedemann and Rudolph Franz found that, for metals, the thermal conductivity is proportional to the temperature multiplied by the electrical conductivity² as shown in Equation 1. In Equation 1, K is the thermal conductivity in W/(m∙K), σ is the electrical conductivity in S/m, L is the Lorenz number (2.44×10-8 V²K-²), and T is the temperature in K.

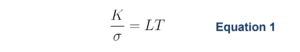
When rearranged to express K as a function of σ, it is evident that the thermal conductivity is directly proportional to the electrical conductivity. The basis for this relationship comes from the fact that both electrical and thermal conductivity are a result of the movement of the same free electrons through the material.

Figure 1: A. A. Approximated thermal conductivity (k) of DNI alloys versus their electrical conductivity values. B.Thermal conductivity of DNI alloys versus their electrical resistivity values. Data collected at room temperature for Figure 1.

The Weidemann-Franz-Lorenz law is not without limitations. The Lorenz number is not perfectly constant for all materials, and it has been experimentally shown that in high purity metals the electrical and thermal conductivities actually increase when the temperature decreases.³ Other experimentation suggests that the Wiedemann-Franz-Lorenz law is limited to validity only at extreme ends of the temperature spectrum.⁴

Holm proposed Equation 2 for an approximate calculation of thermal conductivity.⁵ Here, k is an approximated thermal conductivity value in units of W/cm∙˚C, and ρ is the material resistivity in Ω∙cm. The second term in Equation 2 accounts for an average lattice vibration contribution to the thermal conductivity.

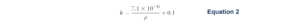
Table 1: Thermal conductivities, resistivities, and percentage nobilities of DNI alloys at various tempers at room temperature.

These relationships are useful in electrical contact design due to the various temperature demands to which electrical contacts are subjected. In Figure 1, the approximated thermal conductivities, k, (W/cm∙˚C) of noble metal alloys made at Deringer-Ney, Inc. are plotted versus their electrical conductivities (%IACS), and resistivities (µΩ∙cm). The direct relationship between thermal conductivity and electrical conductivity is clearly demonstrated. Multiple tempers of some alloys are plotted for comparison as well. Table 1 lists the alloy, temper, thermal conductivity, resistivity, electrical conductivity, and percentage nobility for each data point in Figure 1.

Paliney® is a registered trademark, and Neyoro™ is a trademark of Deringer-Ney Inc.

References:

1. Puglia, M. K. “Bulk Resistivity and Conductivity of Metals” Deringer-Ney Tech Briefs, November 9, 2021. https://www.deeringerney.com/resource-library/.
2. Pitney, Kenneth E. Ney Contact Manual: Electrical Contacts for Low Energy Uses. 1st ed., The J.M. Ney Company, 1973.
3.  Gloos, K., C. Mitschka, F. Pobell, and P. Smeibidl. “Thermal Conductivity of Normal and Superconducting Metals.” Cryogenics 30, no. 1 (January 1990): 14–18. https://doi.org/10.1016/0011-2275(90)90107-N.
4. Rosenberg, H. M. The Solid State: An Introduction to the Physics of Solids for Students of Physics, Materials Science, and Engineering. 3rd ed. Oxford Physics Series 9. Oxford ; New York: Oxford University Press, 1988.
5. Holm, Ragnar. Electric Contacts. Berlin, Heidelberg: Springer Berlin Heidelberg, 1967. https://doi.org/10.1007/978-3-662-06688-1.