Issue 023, December14, 2021

Patrick K Bowen, PhD, R&D Manager

The accurate and precise measurement of elastic constants is challenging, and deviations between reported values and actual material behavior may affect component performance.

Generally, the Young’s modulus (E), Poisson’s ratio (ν), and shear modulus (G) are sufficient for engineering design. This trio of “engineering elastic constants” are interrelated; only two constants are required for the calculation of all three.[1]

Use of engineering elastic constants requires an assumption of material isotropy. In other words, the engineer must assume equal elastic stress-strain behavior in every direction within the material. To account for anisotropy (i.e. directional non-uniformity) of elastic properties, some applications require the construction of a stiffness or compliance matrix. For engineering metals and alloys with cubic crystal structures, three constants are required. Hexagonal crystals require five[1]; however, their determination and use is beyond the scope of this Tech Brief.

Tensile testing provides the most common and accessible measurement of Young’s modulus. However, uncertainty is nominally ±10% by the tensile testing method. The compounded uncertainty includes factors such as:

• elastic stress-strain nonlinearity, or “anelasticity”[2];
• extensometer accuracy and precision; and
• the algorithm used to select the line of best fit for modulus determination.

Specialized equipment and test techniques may reduce this variation to about ±5%. Poisson’s ratio may be measured adding more complex devices, such as two-axis extensometers and/or digital image correlation (DIC). The latter is increasingly common in materials research laboratories. An alternative measurement method based on ultrasonic wave propagation velocity avoids the pitfalls mentioned above. Best practices are found in ASTM E494.[3]

Figure 1: Equipment and supplies for ultrasonic wave velocity measurement.

An ultrasonic thickness gauge may be used for these measurements. Deringer-Ney employs a Olympus 38DL PLUS thickness gauge [Figure 1(A)]. This gauge has sufficient time-of-flight resolution to record wave velocities to 0.0001 in/µs readability (actual measurements are on the 0.1 in/µs order of magnitude). Longitudinal wave velocities are collected with a 20 MHz longitudinal transducer [Figure 1(B)], using a glycerin ultrasonic couplant [Figure 1(C)]. Transverse wave velocities are recorded with help from a 10 MHz normal incidence shear wave transducer [Figure 1(D)], using highly viscous baked honey couplant [Figure 1(E)] to support shear wave propagation.

Respective longitudinal (VL) and transverse (VT) wave velocities are calculated from the round trip time of flight through the material (δL and δT, respectively) and material thickness determined by micrometer measurement (t). This relationship is shown as Equation 1:

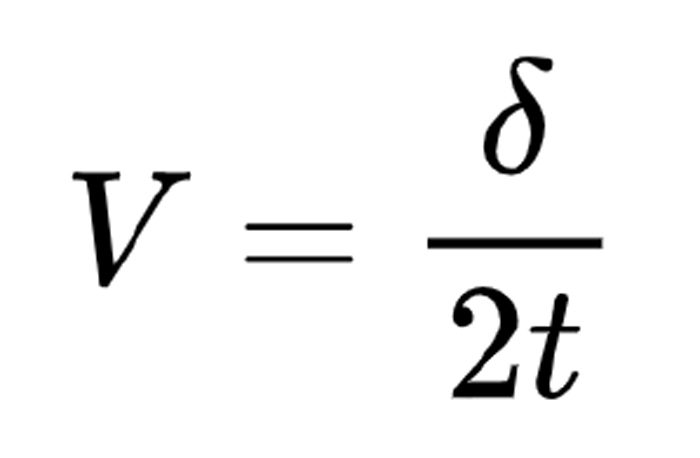
A modern ultrasonic thickness gauge will perform the calculation from Equation 1 automatically. Once the wave velocities are recorded, only the alloy density (ρ) is required to calculate engineering elastic constants using Equations 2, 3, and 4.

Equation 2:

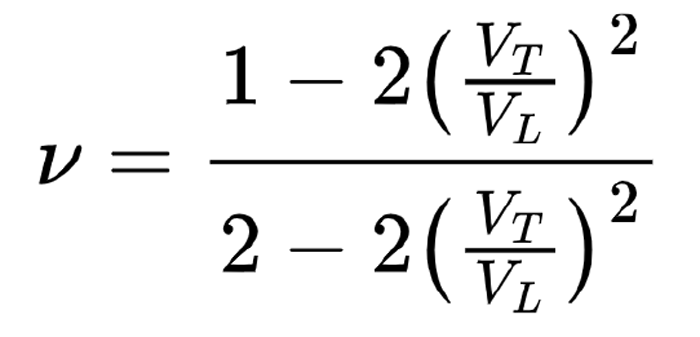
Equation 3:

Equation 4:

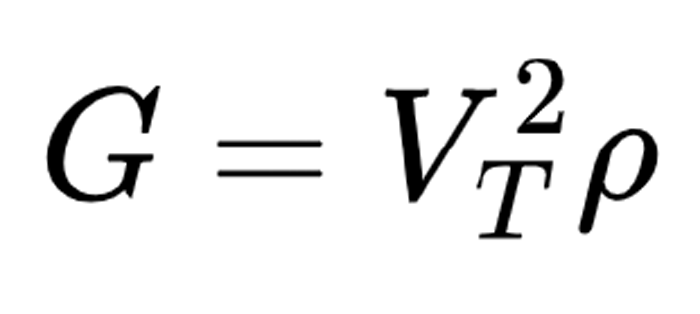
A compilation of engineering elastic constants determined from ultrasonic wave velocities at the time of writing may be found in Table 1.

Table 1: Engineering elastic constants for work hardened noble metal alloys determined by ultrasonic wave velocity measurements, arranged in order of descending Young’s modulus.

Alloy moduli are correlated with their principal constituents. When alloys are ordered by Young’s modulus, platinum-based materials exhibit the highest moduli, palladium-based alloys are in the middle, and gold-based metals are lowest. The ~2.5-fold range of available elastic moduli in materials from Deringer-Ney—as well as various nobilities, conductivities, and hardnesses/strengths—enables considerable design flexibility for electrical contacts and medical components and assemblies.

Note: Paliney® is a registered trademark and Neyoro™ and Deriney® are trademarks of Deringer-Ney Inc.

References:
[1] Bowman K. Mechanical Behavior of Materials. John Wiley & Sons, Inc.; 2004.
[2] Li D, Wagoner RH. The nature of yielding and anelasticity in metals. Acta Materialia. 2021 Mar 1;206:116625.
[3] ASTM E494-20, Standard Practice for Measuring Ultrasonic Velocity in Materials by Comparative Pulse-Echo Method [Internet]. West Conshohocken, PA: ASTM International; 2020. Available from: https://www.astm.org/e0494-20.html